摘要：对于【软件设计师】软考考试而言，试题无疑是最重要的学习资料之一。在软考备考过程中，吃透试题、掌握试题所考知识点、熟悉试题的出题思路，对我们提升分数的效果是最明显的，通过对试题的反复练习，还可以查漏补缺。今天，给大家带来【2015年11月 软件设计师 上午题】部分试题的详解，一起来看看吧~



1、设一个包含n个顶点、e条弧的简单有向图采用邻接矩阵存储结构（即矩阵元素A[i][j]团等于1或0，分别表示顶点i与顶点j之间有弧或无弧），该矩阵中非零元素数目为（）。
A、 e
B、 2e
C、 n-e
D、 n+e

答案:A
答题解析:

用邻接矩阵存储有向图，图中每一条弧对应矩阵一个非零元素，题目中提到一共有e条弧，所以一共e个非零元素。

miao__miao 2016-05-13

请问矩阵是对称矩阵吗，那a-b和b-a都是1，节点数是不是应该是2e?

MegumiIsh 2016-05-14

是不是对称矩阵看图，如果是无向图表示两个顶点直接的关系，那邻接矩阵是对称矩阵。如果是有向图的话又不一样，每一条弧对应矩阵一个非零元素，比如从节点i到节点j有边，则A_ij为一个非零元素。如果从节点j到节点i有边，则A_ji为一个非零元素。题目中提到一共有e条弧，所以一共e个非零元素。

2、已知算法A的运行时间函数为T(n)=8T(n/2)+n2，其中n表示问题的规模，则该算法的时间复杂度为（）
A、 θ(n)
B、 θ(nlgn)
C、 θ(n2)
D、 θ(n3)

答案:D
答题解析:

我们可以假设这个函数为Q(n)=a*n^3+b*n^2+c*n+d(我们假设是一个幂函数，最高次数是三次，假设成什么都可以，但是假设为幂函数大家好理解。)

然后将式子带入得a*(2n)^3+b*(2n)^2+c*(2n)+d=2(a*n^3+b*n^2+c*n+d),然后展开，发现式子会变成

这样：8a*n^3+4b*n^2+2c*n+d=2a*n^3+2b*n^2+2c*n+2d。

对于一个多项式来说，如果等式两边相等，那么每一项（幂数相同，式子中的a、b、c、d均为系数)

都应该相同那么应该：8a*n^3=2a*n^3、4b*n^2=2b*n^2、2c*n=2c*n、d=2d。

很明显如果等式想要相等的话，那么式子中的三次项、二次项、常数项系数应为0

所以这个式子就会变为2c*n,所以Q(n)=2c*n，因为2c为常数，所以可以省去。

这个函数就是一个线性函数，Q(n)=n,然后在将式子回带，Q(n)=n，

那么G(n)=n-1,依旧是线性函数，省略1，

此时G(n)=n，那么T(n)=n^3,所以时间复杂度为n^3

3、已知算法A的运行时间函数为T(n)=8T(n/2)+n2，其中n表示问题的规模，另已知算法B的运行时间函数为T(n)=XT(n/4)+n2，其中n表示问题的规模。对充分大的n，若要算法B比算法A快，则X的最大值为（）。
A、 15
B、 17
C、 63
D、 65

答案:C
答题解析:

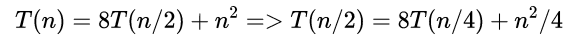
把T(n/2)代入左边可得：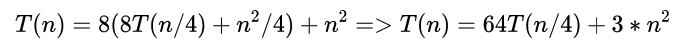

由于n足够大，3*n^2值可以需略，所以X保证是63就能快

查看完整试题>>>